I期临床试验剂量的设计及实施

I期临床试验剂量探索从1989年的3+3设计到现在30年来，由于3+3设计的一些缺点，包括过多受试者分配在低剂量下，不能灵活设定MTD目标水平，MTD估计不准确等，统计学家们提出了很多新的设计方法。

由于I期样本量较小的特点，很多方法都是基于贝叶斯统计。主要包括基于模型的设计(CRM、EWOC、BLRM等)，基于模型辅助设计(mTPI、BOIN、Keyboard等)，基于规则设计i3+3。

今天给大家来介绍一下基于模型辅助设计中的mTPI(modified toxicity probability interval)方法。

本文分为4个部分，第1部分为概率论的一些知识准备，第2部分介绍为剂量探索I期设计中的一些常见概念，第3部分为mTPI的具体实施步骤，第4部分总结mTPI的优缺点，最后将提供SAS code。

一. 概率论知识准备

01 伽马函数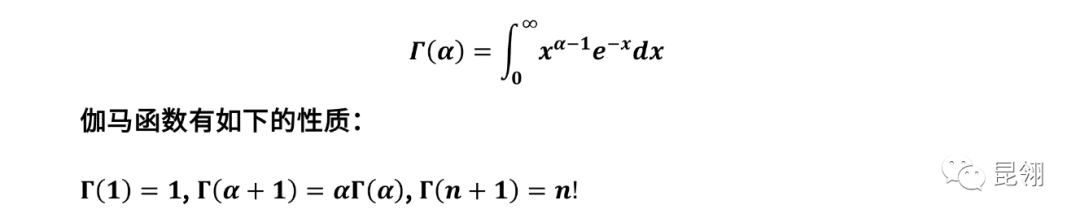

02 伽马分布

03 贝塔函数

04 贝塔分布

05 Beta-Binominal分布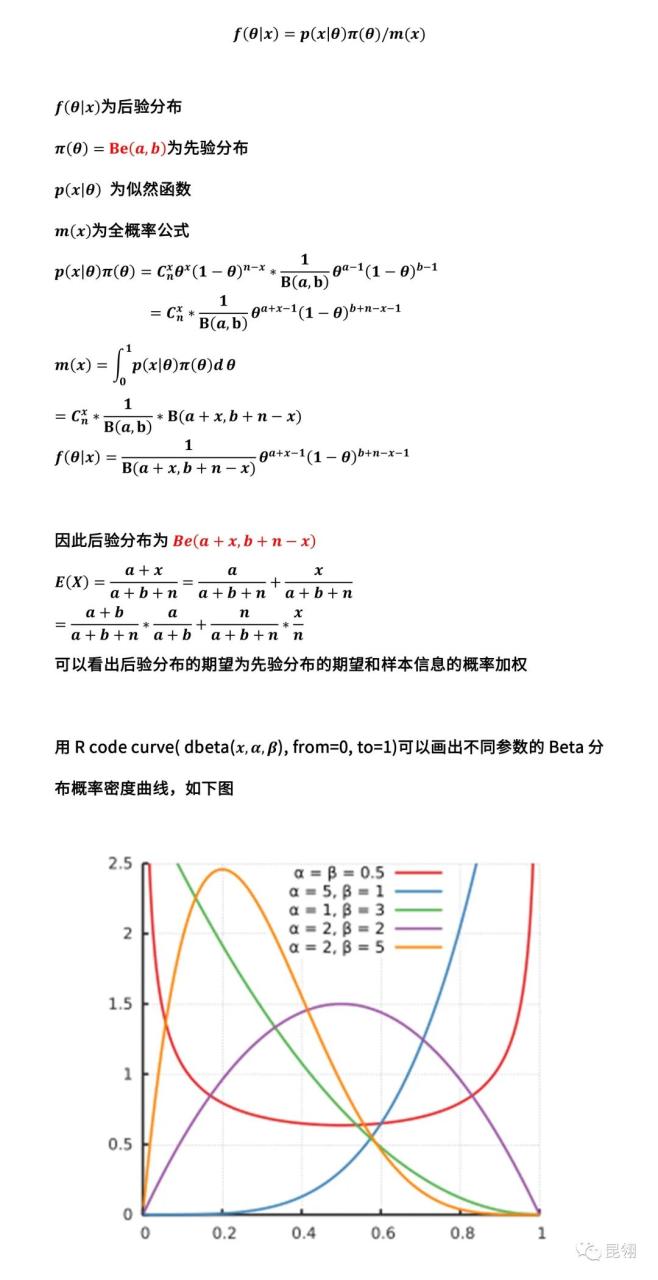

二. 一些常见概念

01 最大耐受剂量MTD（maximum tolerated dose）为毒性概率不超过目标毒性的最高剂量水平

02 目标毒性概率PT（target probability of toxicity），由临床团队确定，通常为0.2-0.3

03 等效区间EI（equivalence interval）,下限为临床可接受的不需要剂量递增的最低剂量，上限为临床可接受的不需要剂量降低的最高剂量，比如当目标毒性概率为0.3时，EI设为[0.25,0.35]

04 剂量限制毒性DLT(dose limit toxicity),需要再方案中详细定义

05 队列大小Cohort Size，一组入多少受试者，注意每个dose level下可以有多个Cohort

三. mTPI具体实施步骤

设有d个待探索的剂量水平，P_i为第i个剂量水平下未知毒性概率，i=1.2…d，假设毒性概率随着剂量水平递增而递增，P₁<P₂≤..P_d这个假设很重要，将会在最后选择MTD的时候用到

定义等效区间EI为[PT-ε₁，PT+ε₂]将（0,1）划分为三个子区间（0，PT-ε₁），（PT-ε₁,PT+ε₂），（PT+ε₂,1）分别为低于MTD，接近MTD，高于MTD

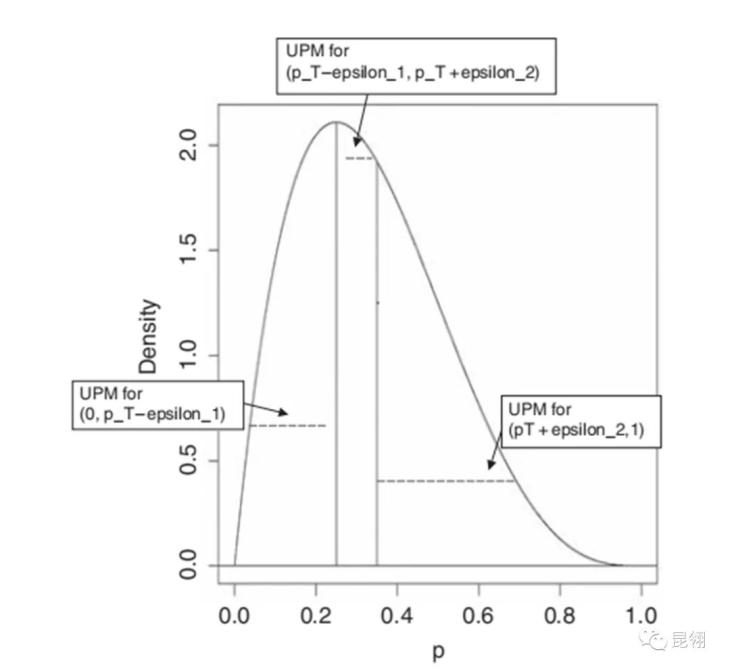
设当前剂量下，有n个受试者，其中有x_i个受试者发生了DLT，假设先验分布为均匀分布U（0，1），根据第一部分的概率论知识可知后验分布为Be（x_i+1,n_i-x_i:+1），此时引入UPM（Unit Probability Mass）概念，对于一个给定的区间和后验分布，UPM=P（区间）/区间长度。分别计算三个子区间对应的UPM大小，
UPM₁=P(p_i<PT-ε₁）/（PT-ε₁），表示（0，PT-ε₁）的UPM；
UPM₂=P(PT-ε₁<p_i<PT+ε₂）/（ε₁+ε₂），表示（PT-ε₁,PT+ε₂）的UPM；
UPM₃=P(p_i>PT+ε2）/（1-PT-ε₂），表示（PT+ε₂,1）的UPM；

用SAS function probbeta可以很容易计算出三个UPM的大小，比如
UPM₁=probbeta(PT-ε₁,x_i+1,n_i-x_i+1)/（PT-ε₁）
如果UPM最大时，则递增到下一个剂量组i+1；
如果UPM，最大时，则维持当前剂量组i；
如果UPM最大时，则降低到下一个剂量组i-1；

一些安全性规则
1）对于第一组受试者，若P(p₁>PT)>ζ（比如取ζ=0.95），则说明最低剂量水平毒性过高，此时停止整个临床试验
2）对于i>1，若P（p_i>PT）>ζ，则说明i剂量水平毒性过高，此时将i剂量及i以上剂量排除

重复上述步骤直到达到所规定的最大样本量或者爬完规定的剂量。可以根据上述规则，事先制定决策表，如通过U-design得到下图

决策表的列表示当前剂量组下入组的受试者人数，行为当前剂量下发生DLT人数。

例如，如果当前剂量组i下入组了3个受试者，当发生DLT人数为0个时，则递增到下一个剂量组i+1；当发生DLT人数为1个时，则继续在当前剂量组i入组受试者；当发生DLT人数为2个时，则下降到前一个剂量组i-1：当发生DLT人数为3个时，则剂量组i及i以上剂量组将被排除，不入组受试者。

根据剂量爬坡情况得到各个剂量水平下的受试者人数和发生DLT人数，然后银据保序回归（isotonic regression）估计MTD。基于模型辅助设计的方法最后选择MTD的时候都会用到保序回归。保序回归简单解释为，给定一系列的真实值X₁,X₂…X_i，对应的权重分别为W₁,W₂…W_i，目的就是找出一系列估计值P₁,P₂..P_i：使得∑₁W_i·（x_i-P_i)²最小，并且P₁≤P₂≤P_i，可以通过PAVA（pool adjacent violators algorithm）算法。PAVA算法：从x₁开始，从左向右移动，当X_i>X_i+1时，则用算其加权平均值替代P_i=P_i+1=（W_i*X_i+W_i+1*X_i+1）/(W_i+W_i+1）

PAVA算法举例

原始序列：9，13，11；结果序列：9，12，12
分析：从9往后观票，观察到11时发生乱序（13>1），停止该轮观察转入吸收元素处理，吸收元素11后子序列为<13，11>，假设权重都为1，取该序列所有元素的平均值得12，故用序列~12，12>替代-13，11。吸收11后已经到了最后的元素，处理操作完成。

原始序列：12，11，10，15；结果序列：11，11，11，15
分析：从12往后观察，观察到11时发生乱序（12>11），停止该轮观察转入吸收元素处理，吸收元素11后子序列为-12，11>。求该序列所有元素的平均值得11.5，由于11.5大于下个待吸收的元素10，所以再吸收10，得序列<12，11，10>。求该序列所有元素的平均值得11，由于11小于下个待吸收的元素15，所以停止吸收操作，用序列<11，11，11>替代<12，11，10> 在模型辅助设计估计MTD时，各个剂量下毒性概率观察值为后验分布的期望 比时假设先验分布为Be（0.05,0.05），x_d和n_d分别为d剂量下发生DLT人数和入则后验分布为Be（x_d+0.05,n_d-x_d+0.05），因此期望P_d=(x_d+0.05)/(n_d+0.1)，P_d为isotonic-transformed后验分布期望，在所有满足n_d>0和P_d≤PT+ε₂条件下，求d=argmini（P_d-PT），如果有多个d存在，那么根据以下规则选择MTD：
a）如果P_d>PT，则选择多个d中的最低剂量为MTD
b）如果P_d·≤PT，则选择多个d中的最高剂量为MTD

假设一个试验4个剂量水平下的结果为n<-c(3，3，7，12），x<-c(0，0，2，3） 其中n为各个剂量水平下的受试者数，×为各个剂量水平下发生DLT数，PT-0.3，EI为[0.25,0.35]，则根据PAVA算法可以得出MTD为剂量4 分析：先分别求出4个剂量下的后验分布期望 P₁=P₂=0.05/(3+0.1)=0.017,P₃=(2+0.05)/(7+0.1)=0.289,P₄=(3+0.05)/(12+0.1)=0.252， P₃>P₄权重为后验分布方差的倒数W₃：=39.44，W₄=69.49，根据PAVA算法，P₃=P₄=（W₃*P₃+W₄*P₄）/（W₃+W₄）=0.265<PT=0.3，因此根据规则将剂量4选为MTD

四. mTPI的优缺点

优点：基于模型辅助设计，可以提前制定决策表，方使临床医生进行剂量上升和下降的判断，估计MTD准确性优于3+3设计。

缺点：受试者暴露于过高毒性的风险较大，比如当前剂量入组6个受试者，3个受试者发生DLT时，mTPI的决策是维持当前剂量，为了解决这个问题又提出了新的设计方法mTPI2、Keyboard，将在下一期进行介绍。

Reference:

1. Ji, Y., Liu, P., Li, Y., & Nebiyou Bekele, B. (2010). A modified toxicity probability interval method for dose-finding trials.

2. https://udesign.laiyaconsulting.com/

3. https://www.trialdesign.org/

SAS完整代码

/*** mTPI: modified toxicity probability interval ***/

dm”log;clear;output;clear;”;

proc datasets lib=work kill nowarn nodetails nolist mt=data;

quit;

data mtpi;

  length decision $2;

  n= 6;

  pt=0.3;/** the target probability of toxicity **/

  epsilon1=0.05;

  epsilon2=0.05;/** the pre-specified define the equivalence **/

  do m=0 to n;/** m means the DLT patients number, n means the treated patients number **/

    /** cumulative distribution function of beta distribution with a=1+m,b=1+n-m **/

    prob1 = probbeta(pt – epsilon1, 1 + m, 1 + n – m);

  prob2 = probbeta(pt + epsilon2, 1 + m, 1 + n – m) – probbeta(pt – epsilon1, 1 + m, 1 + n – m);

prob3 = 1 – probbeta(pt + epsilon2, 1 + m, 1 + n – m);

  * denote a pre-defined threshold for the posterior probability of unacceptably high toxicity, e.g., = 0.95;

  stopprob = 1 – cdf(‘beta’, pt, 1 + m, 1 + n – m);

  /** the unit probability mass(UPM) of each interval **/

  upm1 = prob1 / (pt – epsilon1);

  upm2 = prob2 / (epsilon1 + epsilon2);

  upm3 = prob3 / (1- pt – epsilon2);

      * De-escalate;

        if upm3 > upm1 & upm3 > upm2 then do;

            if stopprob < 0.95 then decision = “D”; 

            else decision = “DU”; 

        end;

        * Escalate;

        if upm1 > upm2 & upm1 > upm3 then decision = “E”;

        * Stay at the same dose;

        if upm2 > upm1 & upm2 > upm3 then decision = “S”;

        output;

    end;

    keep m upm1 upm2 upm3 stopprob decision;

run;

/*** mTPI decision table ***/

%MACRO create_mTPI_table(nmin =,nmax =,dltsmax =,a=,b = ,ptol = ,eps1 = ,eps2 = ,excl = );

DATA mtpi_table(drop = a b ptol eps1 eps2 excl pp escal stabl deesc);

LENGTH n dlts 8 saf $2 idlabel $10;

LABEL dlts = “# DLTs”;

DO n = &nmin. TO &nmax.; DO dlts = 0 TO &dltsmax.;

IF dlts > n THEN saf = ” “;

ELSE DO;

a = %sysevalf(&a.);*prior beta distribution ;

b = %sysevalf(&b.);

ptol = %sysevalf(&ptol.);* the target toxicity probability;

eps1 = %sysevalf(&eps1.);

eps2 = %sysevalf(&eps2.);

excl = %sysevalf(&excl.);* the exclude cutoff value;

* Posterior probability;

pp = 1.0 – probbeta(ptol, a + dlts, b + n – dlts);

* Unit probability mass (UPM);

escal = probbeta(ptol-eps1, a+dlts, b+n-dlts) / (ptol-eps1);

stabl = (probbeta(ptol+eps2, a+dlts, b+n-dlts)

– probbeta(ptol-eps1, a+dlts, b+n-dlts)) / (eps2+eps1);

deesc = (1.0 – probbeta(ptol+eps2, a+dlts, b+n-dlts ))/(1.0-ptol-eps2);

* mTPI’s recommendations: “E”= escalate, “S”= Stay, “D”= de-escalate;

IF escal > stabl and escal > deesc THEN saf = “E”;

ELSE IF stabl > escal and stabl > deesc THEN saf = “S”;

ELSE IF deesc > stabl and deesc > escal THEN saf = “D”;

* “DU” = De-escalate and never use again;

IF pp > excl THEN saf = “DU”;

END;

idlabel = “n=” || strip(put(n, best.));

OUTPUT;

END; END;

RUN;

PROC SORT data=mtpi_table;

BY dlts n;

RUN;

PROC TRANSPOSE data=mtpi_table out=mtpi_table_final(drop=_name_);

BY dlts;

ID n;

IDLABEL idlabel;

VAR saf;

RUN;

* Table output;

ODS HTML;

TITLE “ESD(U)-Table of the mTPI method”;

PROC PRINT data=mtpi_table_final label noobs;

RUN;

ODS HTML CLOSE;

%MEND create_mTPI_table;

%create_mTPI_table(nmin =1,nmax =9,dltsmax =9,a=1,b = 1,ptol = 0.3,eps1 = 0.05,eps2 = 0.05,excl = 0.95);

转自昆翎：